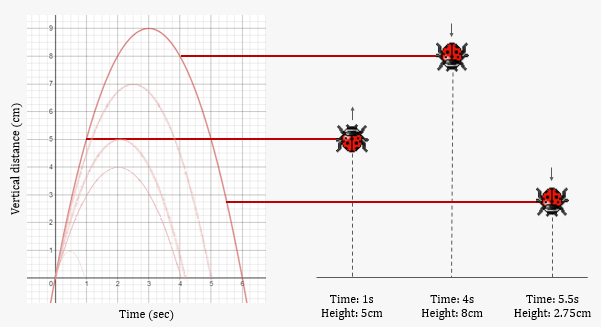
هنگامی که یک حشره به ارتفاع y پرش میکند، موقعیت آن را میتوان به عنوان یک تابع درجه دوم با x به عنوان زمان و y به عنوان فاصله عمودی طی شده ترسیم کرد. به عنوان مثال، برای حشرهای که به ارتفاع ۹ سانتیمتر میپرد و پس از ۶ ثانیه دوباره به زمین بازمیگردد، مسیر آن را میتوان به صورت زیر ترسیم کرد:
یک تابع ایجاد کنید که با توجه به حداکثر ارتفاع پرش عمودی (بر حسب سانتیمتر) و زمان فعلی (بر حسب میلیثانیه)، موقعیت فعلی حشره را به دو رقم اعشار گرد کرده و جهت حرکت (“بالا” یا “پایین”) را برگرداند. اگر حشره از قبل به زمین بازگشته باشد، مقدار ۰ برای موقعیت و None برای جهت حرکت برگردانید.
نمونه ورودی و خروجی
BugJump(9, 1000) ➞ [5, "up"]
BugJump(9, 4000) ➞ [8, "down"]
BugJump(9, 5500) ➞ [2.75, "down"]
نکات
- زمان و موقعیت هر دو از ۰ شروع میشوند.
- حرکت حشره مشابه نمودار x^2 با ضریب -1 است (با آفست های x و y).
Assert.Equal(new object[] { 5, "up" }, Backendbaz.BugJump(9, 1000));
Assert.Equal(new object[] { 8, "down" }, Backendbaz.BugJump(9, 4000));
Assert.Equal(new object[] { 2.75, "down" }, Backendbaz.BugJump(9, 5500));
Assert.Equal(new object[] { 0, null }, Backendbaz.BugJump(9, 7000));
Assert.Equal(new object[] { 5, "up" }, Backendbaz.BugJump(5, 2230));
Assert.Equal(new object[] { 5, "down" }, Backendbaz.BugJump(5, 2240));
Assert.Equal(new object[] { 8.14, "up" }, Backendbaz.BugJump(12, 1500));

وقت بخیر... با داشتن ، یک نقطه و فقط ارتفاع نقطه ماکزیمم ( یا مینیمم ) آیا میشه معادله سهمی رو درست کرد؟! نیاز به اطلاعات بیشتری نیست؟
وقت بخیر
طبق اعدادی که روی نمودار می بینید، باید معادله درجه 2 مربوطه رو بنویسید. ورودی ای که در تابع میگیرید (زمان بر حسب ثانیه)، همون مقدار x ما در نمودار هست. شما باید مقدار y رو طبق معادله ای که می نویسید به دست بیارید.
نگه اینکه بگیم برای تمام حشرات کل مدت زمانی که توی هوا هستند ثابت و برابر یا 6000 میلی ثانیه است
بله، همین فرض رو داشته باشید.
به نظرم سوال اشتباه یا ناقص است ...! فقط برای ارتفاع 9 جواب میدهد.... برای سایر ارتفاع ها جواب را اگر در معادله قرار دهیم با تست های یکی نیست!!!
عذر میخوام، در مورد اینکه زمان رو 6 ثانیه در نظر بگیرید اشتباه گفتم بهتون. در واقع باید شتاب حرکت رو ثابت بگیرید. یعنی در نظر بگیرید که حشره به شکل تابع درجه دوم x با ضریب 1 داره حرکت می کنه. در این مورد همیشه وقتی به حداکثر ارتفاع میرسه، زمانش جذر حداکثر ارتفاع هست. برای ارتفاع 9، زمان میشه جذر 9 یعنی 3 که در کل هم زمان دوبرابر میشه و میشه 6.
الان تمرین رو خودم حل کردم برای تست، مشکلی نداشت و با توجه به این موضوع که توضیح دادم میتونید حل کنید. 🙏
با توضیحات شما کار رو دراوردم ...اما ...
از نظر فیزیکی فرمایش شما اشتباه است...هیچ وقت با حرکت سهمی شتاب حرکت نمی تونه صفر بشه ... همیشه توی حرکت سهمی شتاب حرکت تابع خطی هست از x....اینجا نمودار حرکت سهمی هست یعنی در زمان های یکسان مسافت یکسانی رو داره طی نمی کنه ...باید نمودار قدرمطلق می بود ...مثه یک عدد هشت ...یا هفت ....
البته اون جمله آخر که گفته شده شکل پارابولا رو ترجمه کنید!!! نیاز به مقیاس بندی نیست ...شاید منظور این بوده که مقیاس غیر یکنواخت ارتفاع رو در نظر نگرید در مقابل مقیاس یکنواخت زمان!!! نمی دونم از خودم میگم اینو.... به هر حال این جمله خیلی بر ابهام هست ..مخصوصا که داره خودش میگه پارابولا ...یعنی سهمی! اگه ترجمه بوده از جایی که ترجمه درستی نبوده شاید ....یا من سوادم نمی کشه
ممنون از این که این مشکل رو اطلاع دادید. 🙏
کاملاً درست می فرمایید. نمودار کمی نامفهوم بود. عکس و توضیح رو کمی تغییر دادم که مشخص تر باشه.